Introduction to SSAPRE

I took a course on optimizing compilers at Lund University this autumn. The course included a project in which the students, in groups of two, implemented some of the optimizations that were covered during the course. The optimizations were implemented in a simple subset-of-C compiler, and the goal was to minimize the number of clock cycles for a certain benchmark. The resulting code was run on a simulator.

I worked together with Manfred Dellkrantz, and although we were not originally planning to put such a huge amount of effort into the contest, we soon became obsessed with implementing as many optimizations as possible.

The top three groups from each year are listed on the course webpage. We placed at an all-time 1st place for the particular benchmark used this year! (Update: the benchmark was switched after one more year using the same benchmark)

For our project I implemented an optimization that is described in the paper Partial Redundancy Elimination in SSA Form by Robert Kennedy et al. in TOPLAS, May 1999. In this blog post I will attempt to describe what this optimization does, and how it works.

Partial Redundancy Elimination

Partial Redundancy Elimination is a compiler optimization which aims to remove redundant computations in a program. A program with (partial) redundancies may look like this:

Example 1

if (a < c) {
    c = a+b;
}
a = a+b;

In this example the expression a+b is partially redundant: if execution enters the then-clause of the if-statement, the expression will be evaluated twice. This redundancy can be eliminated by introducing a new instance of the same expression and storing the result in a temporary:

if (a < c) {
    c = a+b;
    t = c;
} else {
    t = a+b;
}
a = t;

Now the expression a+b is only evaluated once, regardless of which execution path the program takes.

SSAPRE is an algorithm for redundancy elimination on programs in Single Static Assignment (SSA) form (note: without critical edges). The output of SSAPRE is another program on SSA form where redundant expressions from the previous program have been replaced by temporaries on SSA form.

The SSAPRE Algorithm

Kennedy et al. present two different versions of SSAPRE. One less efficient but perhaps simpler version and another more efficient version. Personally, I thought the simpler version caused more special cases than the efficient version. I did implement the simpler version first, but I consider that to have been a waste of time since it was much easier to optimize full nested expressions with the more efficient version, and it took less time for me to implement.

I will be very brief in the description of SSAPRE here, so if you need more information I can only suggest that you read the original paper by Kennedy et al. Also, I apologize for any errors I may have made here.

Terminology

Each expression in the original program, such as a+b in the above example, is called a real occurrence of some computation. Two occurrences belong to the same computation if they have the same operands and the same operator.

Besides real occurrences there exist Φ occurrences, Φ operand occurrences and exit occurrences.

Each occurrence also has a redundancy class. The redundancy class is similar to the SSA version of variables in SSA form. Two occurrences that occur in places where the expression returns the same value may have the same redundancy class, it is possible that they do not but two occurrences with equal redundancy class will never return different results.

Φ occurrences are very similar to φ functions for SSA variables. Φs occur at the beginning of basic blocks where different values of an expression meet. The Φ selects a value for the expression based on which predecessor control has come from. A Φ can be regarded as representing the latest redundancy class of the computation, just as a φ would represent the latest version of an SSA variable.

Φ operand occurrences are at the end of basic blocks which have a successor with a Φ. A Φ operand is ⊥ (bottom) if the expression is not evaluated/used after a redefenition of one of its variables (before the Φ which the Φ operator is an operand of).

Exit occurrences are really only used to initialize downsafety. More on that later.

Φ insertion

The first step of SSAPRE is to insert Φ occurrences. To quote Kennedy et al.

A Φ for an expression is needed whenever different values of the same expression reach a common point in the program.

This is very similar to φ insertion in regular SSA transformation, and it can be implemented similarly. A Φ must be inserted in each basic block on the iterated dominance frontier of the real occurrences of a computation, and the iterated dominance frontier of each of its operands’ (re)definitions.

Occurrence Renaming

The redundancy class for occurrences is assigned in a step called Rename, which again is very similar to the SSA renaming algorithm.

Rename walks over a list of occurrences in dominator tree pre-order. For each real occurrence it encounters, it assigns the latest redundancy class. For each Φ it assigns the next redundancy class, and for each Φ operand it assigns either the latest redundancy class or ⊥. There are some important special cases here, but otherwise that’s the general idea.

Inserted Occurrences and Downsafety

In some places, as in Example 1, we might want to insert a real occurrence for a computation. This can only be done if the Φ which the inserted occurrence would be an operand of is downsafe. A Φ is downsafe if each path from the Φ to program exit or a redefinition of one of the operands sees a use of the expression. As Kennedy et al. puts it:

A Φ is not down-safe if there is a control flow path from that along which the expression is not evaluated before program exit or before being altered by redefinition of one of its variables.

If an evaluation of some expression is inserted and is downsafe, we know that we are not introducing expressions into the program which would otherwise not have been evaluated and thus are not introducing new redundancy or exceptions.

If we look at the above example program we can see that in the block right after the if-statement there needs to be a Φ for a+b. This Φ must be downsafe since it has a use later in the same basic block.

To compute downsafety we initialize certain nodes as not downsafe then propagate the not downsafe property upwards in the Control Flow Graph (CFG).

Availability of Occurrences

A Φ occurrence has the property ‘will be available’ at some point in the program if the value of the expression is needed, the Φ is downsafe, and it can not be evaluated later.

The availability, more precisely the ‘will be available’ property of an occurrence is computed by first calculating ‘can be available’ and ‘later’. I won’t describe how these are calculated since it is quite tedious.

Finalizing SSAPRE

When finalizing SSAPRE each computation receives a temporary variable. This temporary is SSA-versioned so that each version of the temporary corresponds to a redundancy class. Occurrences are either:

• inserted
• saved
• reloaded

Φ operands are inserted if they are not available (either ⊥ or defined by Φ which does not satisfy can be available and has no real use).

An occurrence needs to be saved if it is not redundant and can not fetch its value from the temporary.

Occurrences are reloaded when the latest version of the temporary corresponds to the correct (i.e. same as the defining occurrence) redundancy class.

Practical Considerations

SSAPRE uses a worklist of computations to be optimized. The initial pass of SSAPRE collects computations from the program (based on real occurrences) and puts these into the worklist. During SSAPRE more expressions may become eligible for optimization, if so they are put in the worklist. SSAPRE can optimize each computation independently of the others, this means that large parts of SSAPRE can be parallelized.

Nested Expressions

SSAPRE can optimize nested expression trees efficiently by first optimizing simple expressions and then expressions which use those as operands. Depending on the program representation passed to SSAPRE this can be done a couple different ways.

The representation I had to work with in our compiler project was a three address code representation. Some of the expressions would only use symbols and/or constants as operands, while others had one or more temporaries. These temporaries were marked as sub-expression temporaries. When new temporaries were produced through reloaded and saved occurrences, the expressions which contained the new temporaries were made eligible for optimization if they had no other sub-expression temporary operands.

If using a worklist of computations, it is quite easy to enable optimization of nested expressions.

A full SSAPRE Example

Let’s say we want to optimize the following code:

Example 2:

a = 1;
b = 3;
c = 0;
d = 20;
do {
    if (c > 0) {
        put(c*(a+b));
        a = a+1;
    }
    c = a+b;
    put(d*3);
} while (c < d);

This code can be represented by the following CFG:

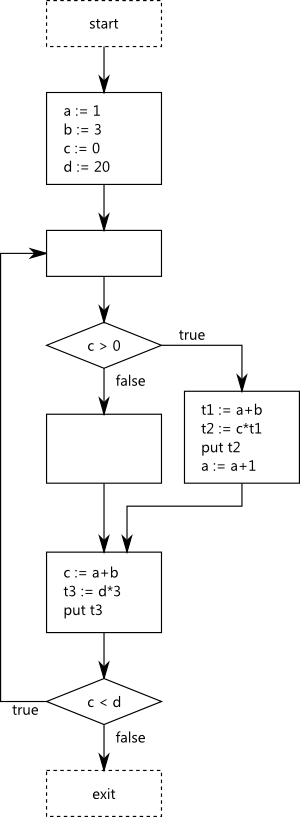
The first task is collecting occurrences. I’ve named the occurrences according to the scheme where the digit is the occurrence id. Temporaries have the letter t. The expression c*t1 is not eligible for optimization since one of its operands is a sub-expression temporary.

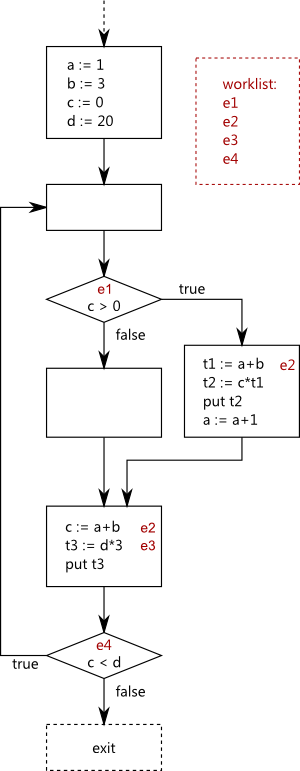
Now we insert Φ occurrences at the iterated dominance frontiers of each real occurrence and each (re)definition of an operand of any computation. The operands are not known at this point:

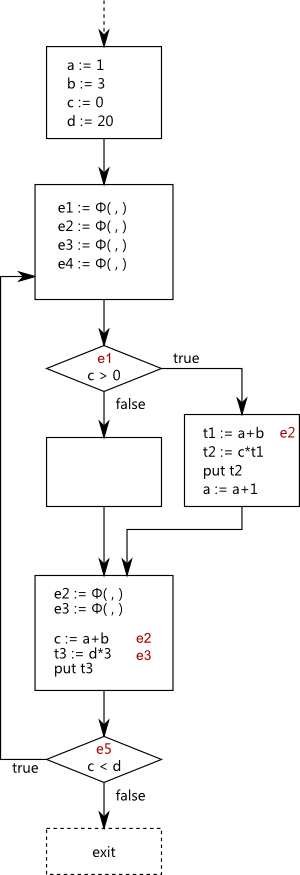
During the Rename step redundancy classes are assigned. Redundancy classes are indicated as the last digit in the occurrence names (e1_3 has redundancy class 3). We can now decide which Φ operands are ⊥ or where they are defined. The dotted arrows in this graph show where the Φ operands for computation e2 are defined. A Φ operand is ⊥ here only if there is a redefinition of one operand without subsequent re-evaluation of the expression. As we can see the second Φ for e2 gets its first operand from e2_0 since there is no redefinition in the else-clause of the if-statement. The second operand is ⊥ since there is a redefinition of the operand a in the then-clause of the if-statement but no subsequent use of the expression.

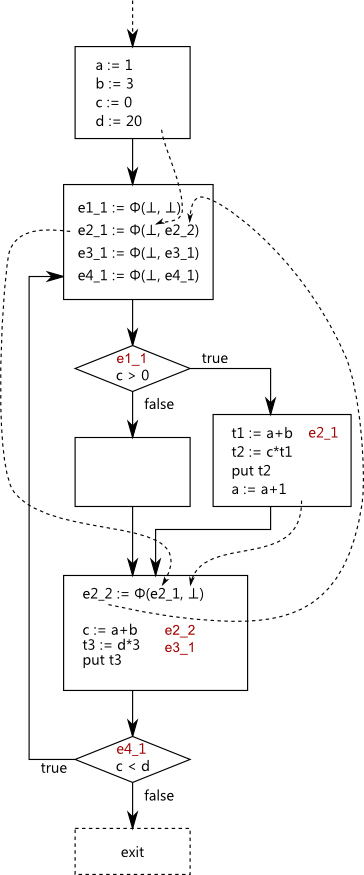
While computing downsafety we find that all occurrences except one are downsafe. The single not downsafe occurrence is the Φ for e4. This is not downsafe since it has no use before the redefinition of c.

Only one occurrence satisfies later - the Φ for e1. It satisfies later since both operands are ⊥.

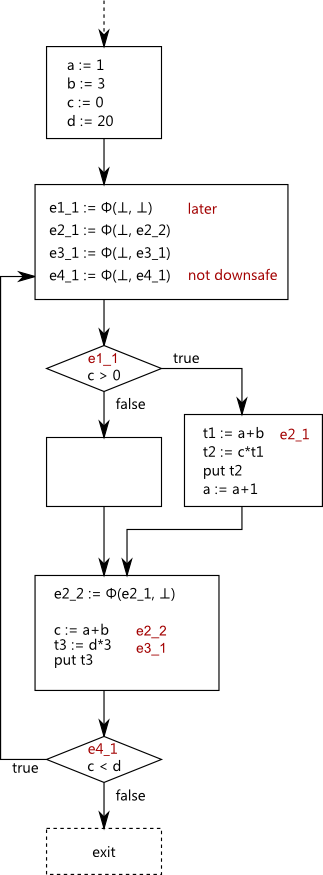
The Φs for e1 and e4 can be discarded since they will not be (made) available.

Now we need to insert those Φ operands which are ⊥ operands of a Φ which satisfies will be available. All the remaining Φs satisfy will be available:

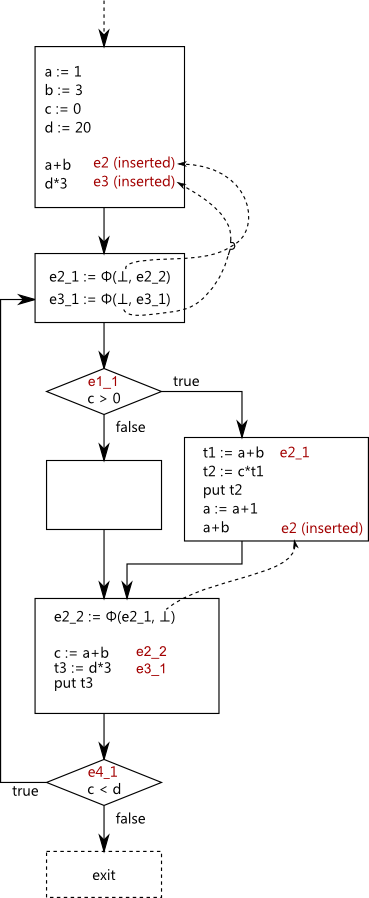
To finalize SSAPRE, we replace each Φ by a φ and insert our new temporaries for each occurrence.

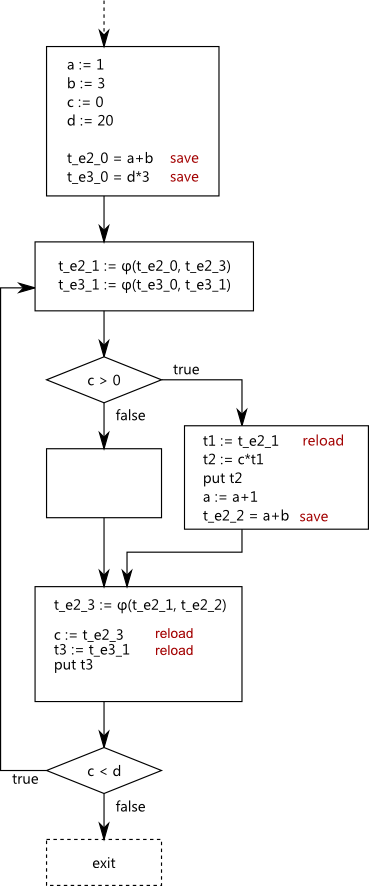
After copy propagation we get a new expression, c*t_e2_1, which is eligible for optimization. It is put in the worklist, however it turns out that nothing can be done with it. So, we are done.